00:00
-00:00
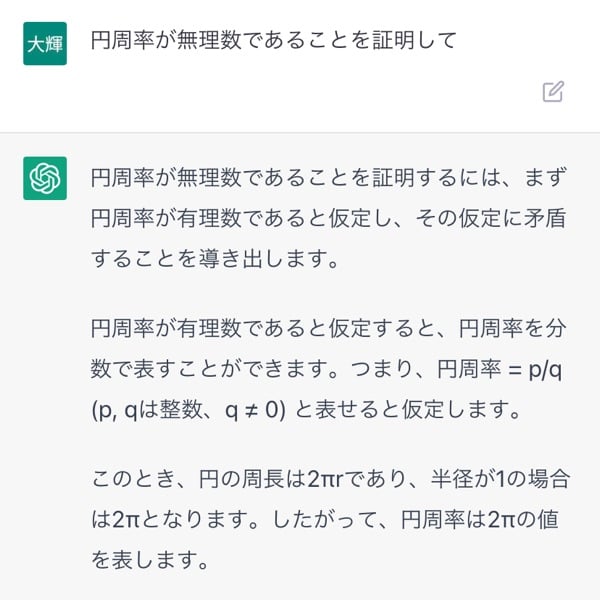
chatGPTになぜ円周率が無理数なのか聞いてみた
円周率が無理数であることを証明するには、まず円周率が有理数であると仮定し、その仮定に矛盾することを導き出します。
円周率が有理数であると仮定すると、円周率を分数で表すことができます。つまり、円周率 = p/q (p, qは整数、q ≠ 0) と表せると仮定します。
このとき、円の周長は2πrであり、半径が1の場合は2πとなります。したがって、円周率は2πの値を表します。
さらに、有理数p/qを代入すると、2π = p/q となります。この式をqで両辺をかけると、2πq = pとなります。
ここで、左辺の2πqは整数であり、右辺のpも整数です。つまり、有理数p/qを用いた円周率の表現において、pは整数で表されることになります。
しかし、円の面積の公式により、円周率は正確に表現することはできません。したがって、円周率は有理数で表すことができないことになり、仮定に矛盾が生じます。
つまり、円周率は有理数で表すことができない無理数であることが証明されます。このように、円周率が無理数であることは、代数的に証明することができます。
2023年4月8日
このチャンネルの新着放送
おすすめの放送
stand.fmの無料アプリでもっと便利に
放送が更新されたらプッシュでお知らせされるので最新の放送を聞き逃さない。
バックグラウンド再生で他のアプリを使用しながら、放送やライブが聴ける。
放送やライブ、コミュニティでコメントが送れて配信者とコミュニケーションができる。
アプリだけでかんたんに音声を収録して投稿できて音声の編集もできる。
stand.fmメディア
JASRAC許諾番号
9024598002Y31016
9024598004Y31016
NexTone許諾番号
000006134
© 2026 stand.fm, Inc.